紅黑樹

概念介紹

樹的搜尋 (Tree Search)，一直是電腦科學領域的重要演算法，當中探討了樹可能遇到的問題：樹成長時可能偏重於特定一邊，即不平衡 (Unbalance) 的現象。二元樹是常見且廣泛使用的一種樹，面臨這樣關乎運氣、可能退化成連結串列 (Linked List) 的潛藏缺點，在使用上免不了讓人擔心效能是否能常保順暢。此外，在一些應用上，可能不期望這樣不平衡的可能性發生，所以具有自動平衡左右數量分布效果的演算法早在約 1962 年便被發表出來，稱為 AVL 樹 (Adelson-Velsky and Landis Tree, AVL Tree)。這種平衡成長的二元搜尋樹 (Binary Search Tree, BST) 被歸類稱為自平衡二元搜尋樹 (Self-Balancing Binary Search Tree)。

規則特性

接下來，要介紹同歸為自平衡二元搜尋樹的紅黑樹 (Red-Black Tree, RBT or RB Tree) 對平衡性的要求比 AVL 樹還寬鬆。紅黑樹是利用節點顏色來檢視二元樹每條延展的路徑高度是否差不多，因此發明者訂立了以下幾點規則。

紅黑樹規則

樹上的每個節點 (node) 只能是紅色或黑色

根節點 (root) 一定要是黑色

葉節點 (leaf) 一定要是黑色的空值 (NULL)

紅色節點的兩個子節點 (child) 一定要是黑色 (亦即不能有兩個紅色節點相連，注意：黑色節點的子節點顏色沒有限制)

從任何節點出發，其下至葉節點所有路徑的黑色節點數目要相同

滿足上述規則的二元樹，相比一般的二元樹更能保持平衡性，往後套用二元樹的算法來查找資料時能更快速、方便地到達目的地，套用運算的時間複雜度為 O(log n)，這是因為紅黑樹保證最長路徑不會超過最短路徑的兩倍。

基礎操作

因為紅黑樹也是二元樹的一種，所以例如：新增節點、刪除節點、查詢節點等針對紅黑樹的操作與二元樹的操作前段演算法相同，只是在每次操作完畢之後可能會讓樹的結構改變而可能無法滿足成為紅黑樹的性質，進而可能不具有平衡的性質。

複習小教室：Operations on Binary Search Tree

常見的操作包含：SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR，其中搜尋節點 (Search)、找最大節點 (Maximum)、找最小節點 (Minimum) 較單純，不多介紹。這邊想多著墨於找尋上位者 (Successor)與下位者 (Predecessor)的操作上，這與之後新增 (Insertion)與刪除 (Deletion)節點的操作具有高度關聯：

Successor(z)：尋找數列的下一個數字 (下位者)。如果右子樹非空，則找右子樹中最小的節點；如果右子樹為空，則往回找第一個比自己大的祖先。

Predecessor(z)：尋找數列的上一個數字 (上位者)。如果右子樹非空，則找右子樹中最大的節點；如果右子樹為空，則往回找第一個比自己小的祖先。

Deletion(z)：刪除特定節點，由子節點的三種情況來討論演算法。沒有子節點或只有一個子節點的時候，直接將該節點刪除，其父節點則直接連接至其子節點(或為NULL)上。但有兩個子節點時，則需要先找到欲刪除節點的下位者是誰，將下位者與欲刪除節點的數值交換，再將下位者(已換成欲刪除節點數值)刪除，其中會將下位者的父節點與下位者的子節點相連 (有兩個子節點時，一般是以右邊最小的子節點、或者左邊最大的子節點來遞補)。

為了在操作後仍是一棵紅黑樹 (滿足上述五項規則)，以下有兩項基本運算可以用來幫助調整樹狀結構以滿足紅黑樹的規則，這兩個運算分別為變色與旋轉 (左旋、右旋)。

首先是變色，這個運算很容易理解，就是將當前顏色改變成另一個顏色，例如紅色改成黑色。
但是很多時候用到的運算是旋轉，如下是以節點 P 為中心進行旋轉運算。

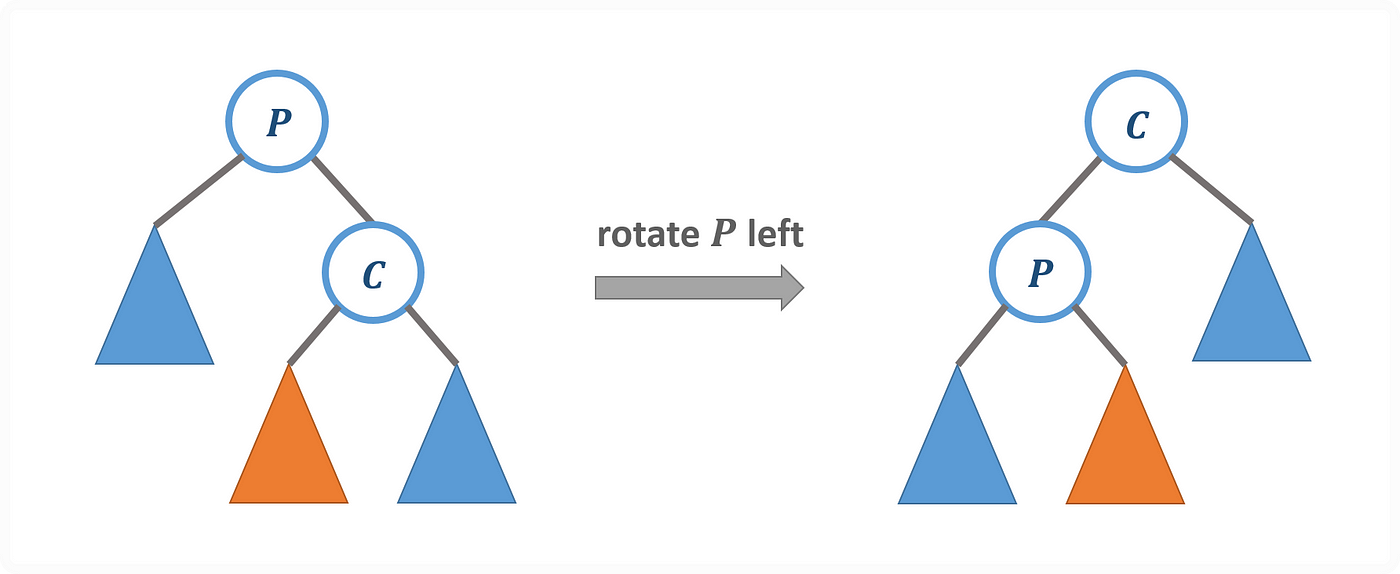
Left Rotation on Node P

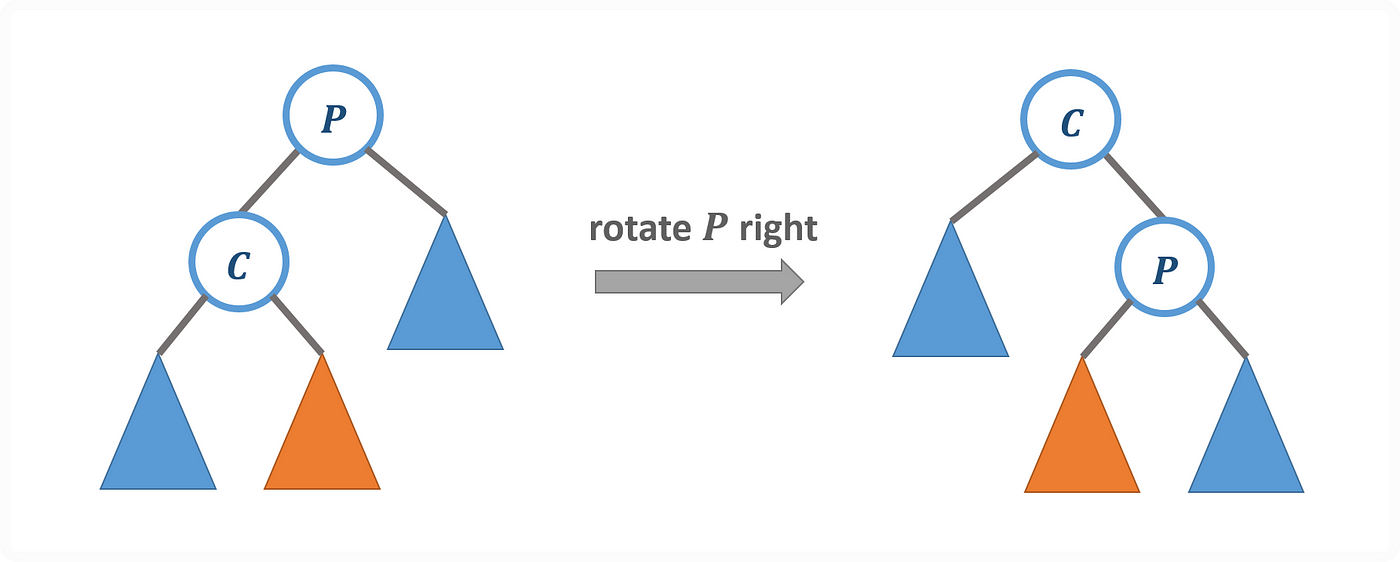
Right Rotation on Node P

基本上維持紅黑樹的演算過程都是由變色與旋轉依次組成。總結來說，紅黑樹的新增與刪除操作是先透過一般二元樹的新增與刪除操作後，再從遞補的節點開始向上進行紅黑樹性質維護。

接下來，直接用例子演示走過一遍新增與刪除節點的演算法更能了解到變色與旋轉的作用為何：

新增 (Insertion)

在新增操作上，新插入的節點一律都為紅色，目的是希望紅黑樹維持規則 5 的約束，但也可能會違反除了規則 5 以外的其他規則，所以作完二元樹新增節點的操作後，需要以新增的節點開始向上檢查紅黑樹是否符合各項規則，修正紅黑樹的演算法可能會有以下幾種情境，因應不同情境會採取不同的修正過程：

情境一：紅黑樹為空，插入紅節點後成為根結點，會違反規則 2，需將該節點改為黑色，即可完成紅黑樹維護。

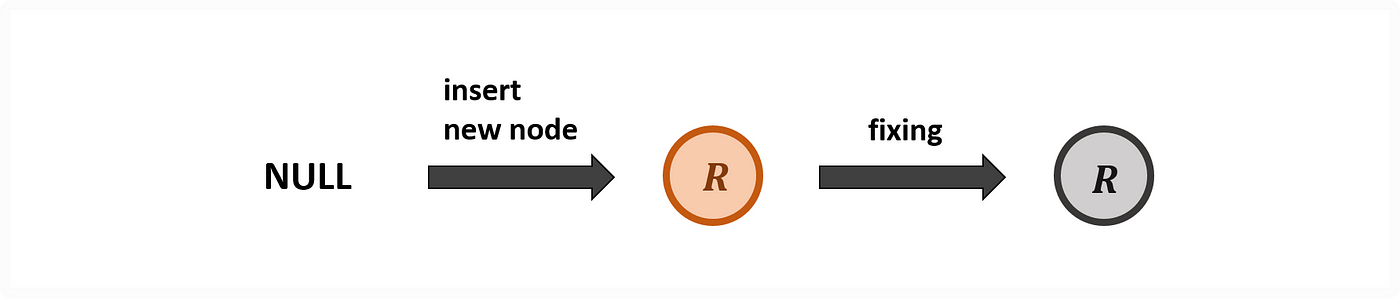
Case 1: Red Node on the Empty RB Tree
情境二：在黑節點上與紅節點 z 相接，不違反任何規則，無須作其他調整。

Case 2: Red Node on a Black Node
情境三：在紅節點上與紅節點 z 相接，會違反規則 4。從自己開始維護，若叔叔節點為紅色，則先將父節點塗黑，用以保持規則 4，但這時會違反規則 5，所以須再將祖節點與叔節點分別塗成紅色和黑色。接著再從祖節點繼續往上檢查維護。

如圖片，可以看到最後的結果違反規則 4，該情境符合情境四所示，其父節點與自身皆為紅色，所以下一輪會再以對應的流程處理。

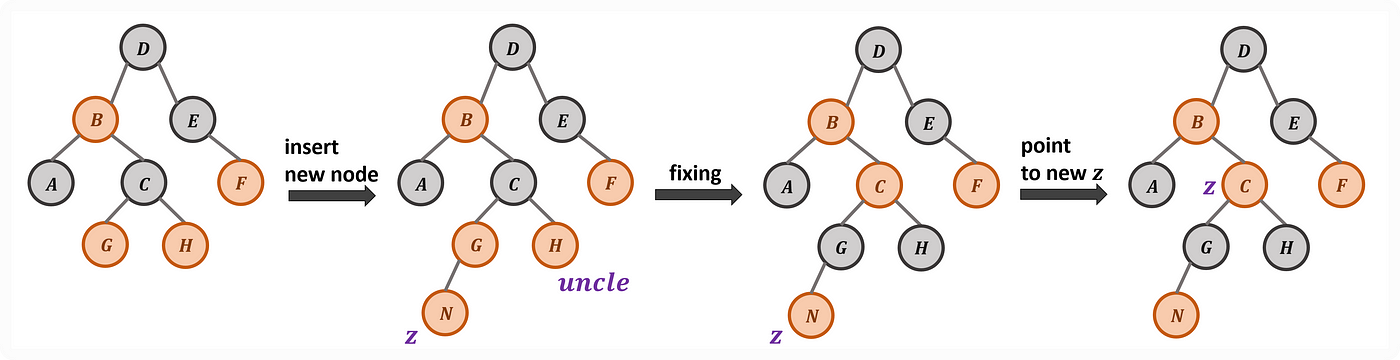
Case 3: Red Node on a Red Node with its Red Uncle Node
情境四：在紅節點上與紅節點 z 相接，會違反規則 4。從自己開始維護，若叔叔節點為黑色且自己位置在父節點右邊的狀況，則先以父節點進行左旋，形成情境五，再作為情況五進行下一輪的處理。

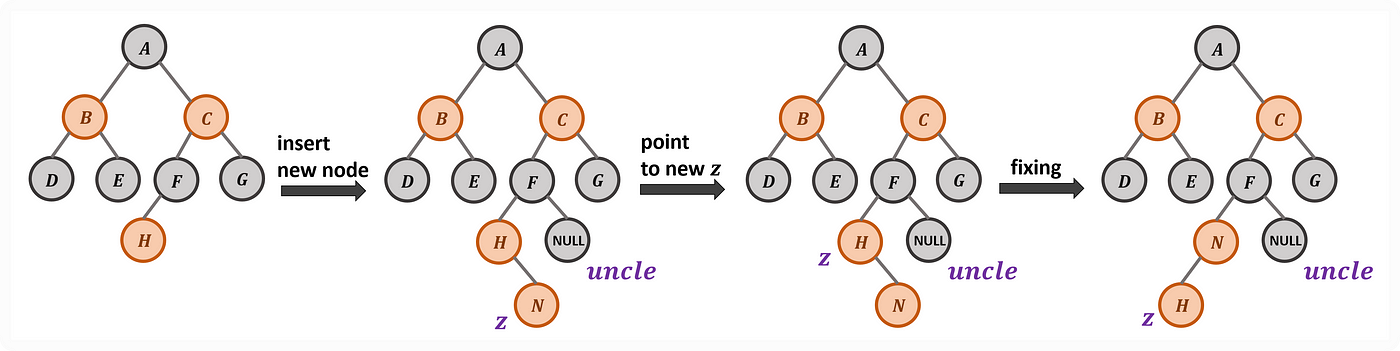
Case 4: Red Node on the Right Side of Red Node with its Black Uncle Node
情境五：在紅節點上與紅節點 z 相接，會違反規則 4。從自己開始維護，若叔叔節點為黑色且自己位置在父節點左邊的狀況，則先將父節點改為黑色，用以保持規則 4，但這時會違反規則 5，所以須再將祖節點塗成紅色，接著再以祖節點進行右旋，即能完成維護。(直覺上，節點 F 的左邊路徑會多一個黑色，可以透過右旋把黑色轉掉)

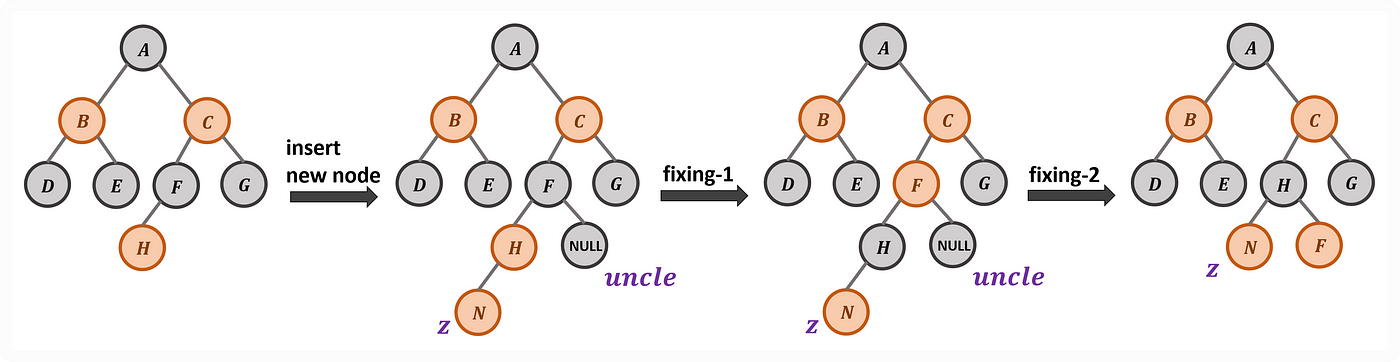
Case 5: Red Node on the Left Side of Red Node with its Black Uncle Node

刪除(Deletion)

在刪除操作上，刪除一個節點時可能也會違反規則，所以作完二元樹刪除節點的操作後，視需要以遞補節點開始向上檢查紅黑樹是否符合各項規則，修正紅黑樹的演算法可能會有以下幾種情境，因應不同情境會採取不同的修正過程：

情境一：刪除紅節點，不違反任何規則，無須進行維護。

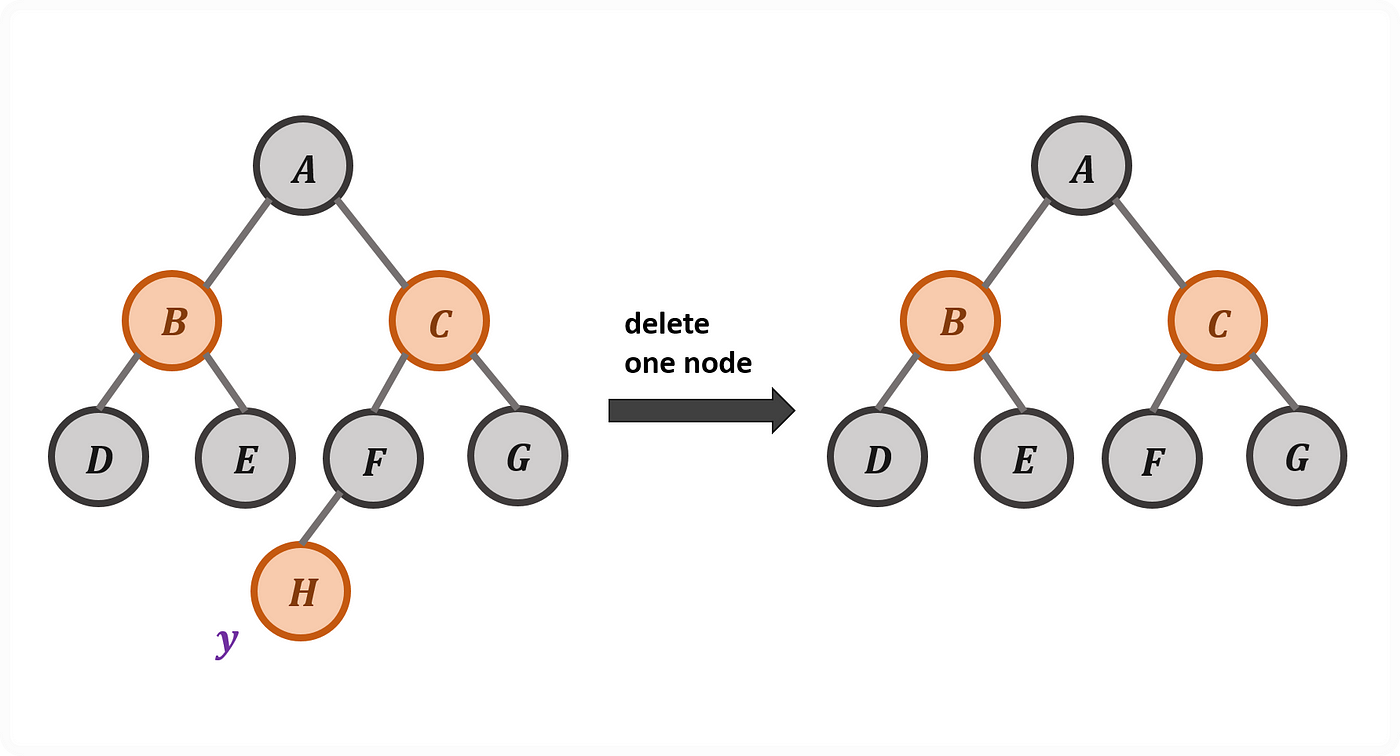
Case 1: Deletion on Red Node
情境二：刪除節點為黑色需要進行維護。刪除黑節點後，如果遞補上來的節點為紅色時，因為黑節點被刪除會違反規則 5，所以直接將遞補的紅節點塗黑即可。或者，如果維護點在根結點時，如果根節點為紅色，這時則違反規則 2，直接將根節點塗黑即可。

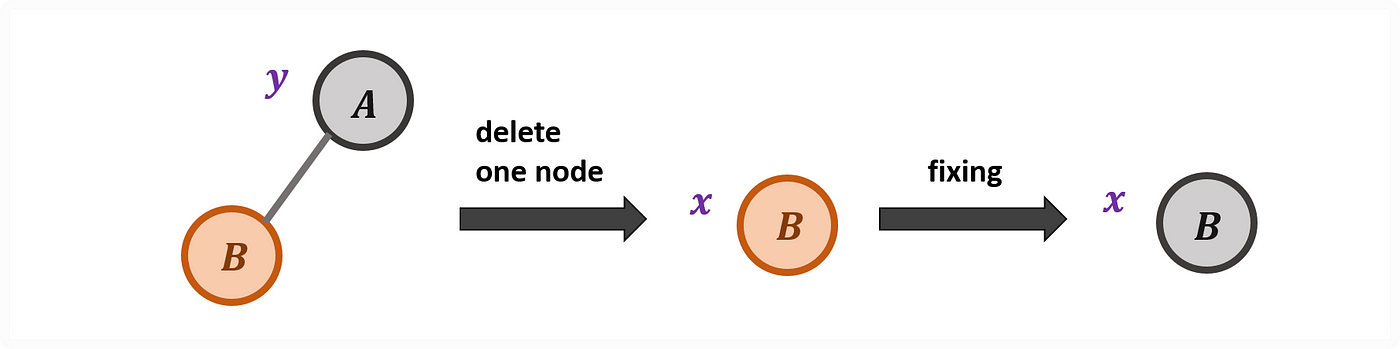
Case 2: Deletion on Black Node with Red Node Compensation
情境三：刪除節點為黑色需要進行維護。刪除黑節點後，如果遞補上來的節點為黑色時，需要視情況補足路徑上缺失的一個黑色，會以遞補節點作為當前節點開始進行維護：

兄弟節點若是紅色，則將兄弟節點塗黑、父節點塗紅、再以父節點為基準左旋 (因為節點 C 的左邊路徑會少一個黑色，直覺會是透過左旋把黑色補起來)。但是可以發現現在的紅黑樹還是違反規則 5，雖然無法完全解決問題，但是遞補節點的兄弟節點改變了，可以新情境再下一輪進行對應的修正。

Case 3: Deletion on Black Node with Black Node Compensation and Red Sibling Node
情境四：刪除節點為黑色需要進行維護。刪除黑節點後，如果遞補上來的節點為黑色時，需要視情況補足路徑上缺失的一個黑色，會以遞補節點作為當前節點開始進行維護：

兄節點若是黑色，且兄節點之左節點與右節點同為黑色的時候，則將兄節點塗紅。這時若父節點為紅色則結束修正後將父節點塗黑即可，但是如果父節點為黑色，則需要再從父節點開始進行修正 (因為也要照顧到父節點的兄弟子樹，看看是否也滿足規則 5)。

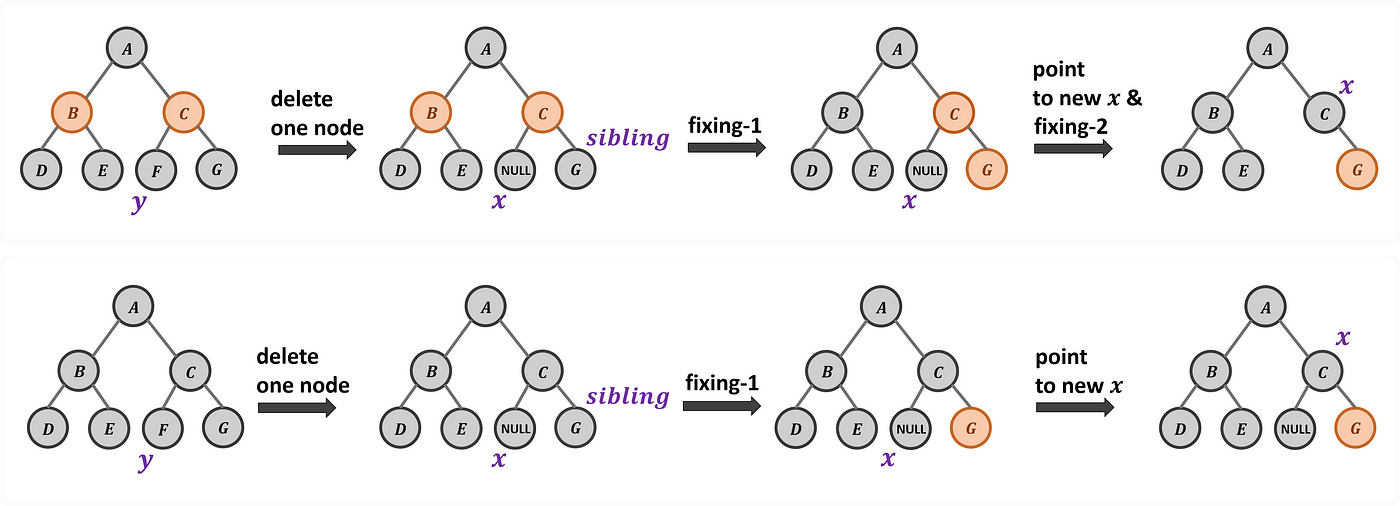
Case 4: Deletion on Black Node with Black Node Compensation and Black Sibling Node with its Two Black Child Nodes
情境五：刪除節點為黑色需要進行維護。刪除黑節點後，如果遞補上來的節點為黑色時，需要視情況補足路徑上缺失的一個黑色，會以遞補節點作為當前節點開始進行維護：

兄節點若是黑色，且兄節點之左節點為紅色、右節點為黑色的時候，則將兄節點塗紅、兄節點之左節點塗黑，再以兄節點為基準右旋，接著再進行下次的修正 (若採用左旋會變成相同情境，所以只好右旋，才可能跳離循環)。

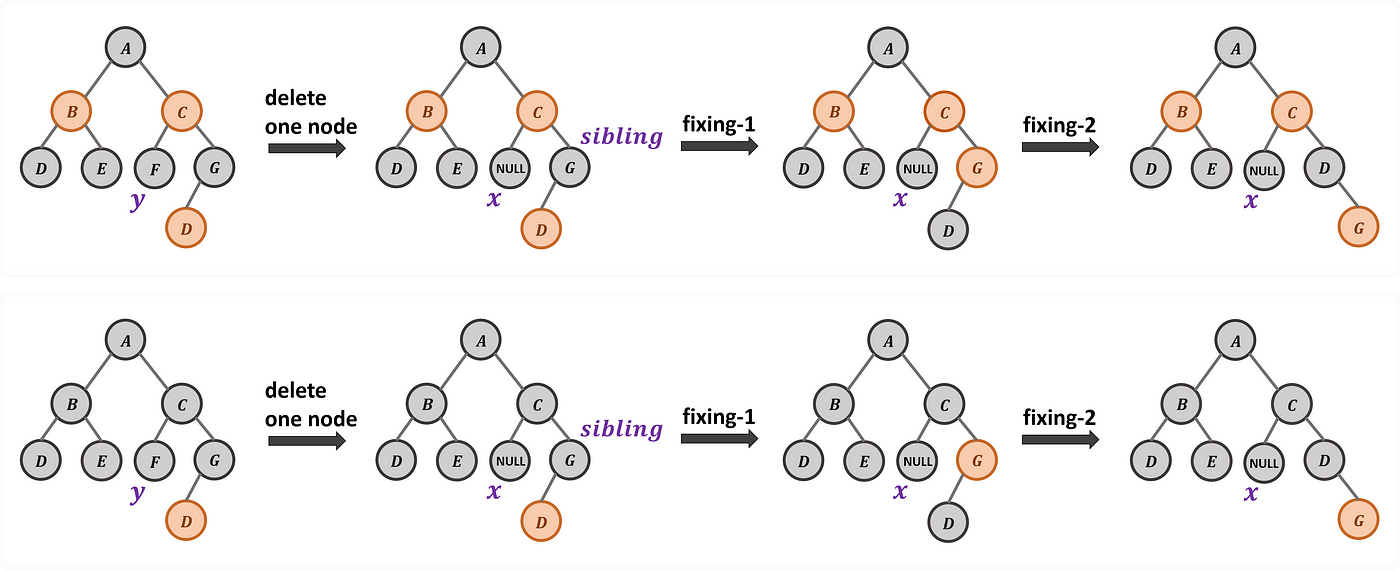
Case 5: Deletion on Black Node with Black Node Compensation and Black Sibling Node with its Red Left Child Node
情境六：刪除節點為黑色需要進行維護。刪除黑節點後，如果遞補上來的節點為黑色時，需要視情況補足路徑上缺失的一個黑色，會以遞補節點作為當前節點開始進行維護：

兄節點若是黑色，且兄節點之右節點為紅色的時候，則將兄節點塗成與父節點相同的顏色、父節點塗黑、兄節點的右節點塗黑，再以父節點為基準左旋即可。(透過左旋與塗色操作將右邊的黑色往左調整、並將右邊紅點塗黑補足缺失，希望符合規則 5 來讓每條路徑上黑色節點的數量一致)

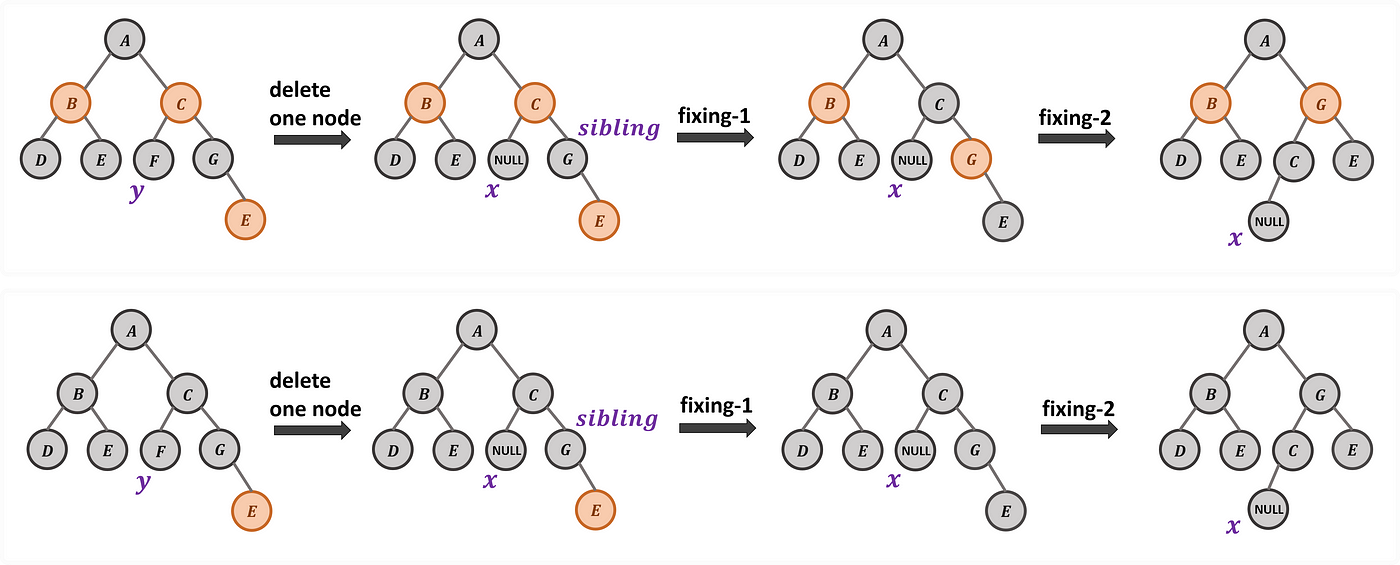
Case 6: Deletion on Black Node with Black Node Compensation and Black Sibling Node with its Red Right Child Node