給自己的筆記：傅立葉轉換

DFT與DTFT的差異

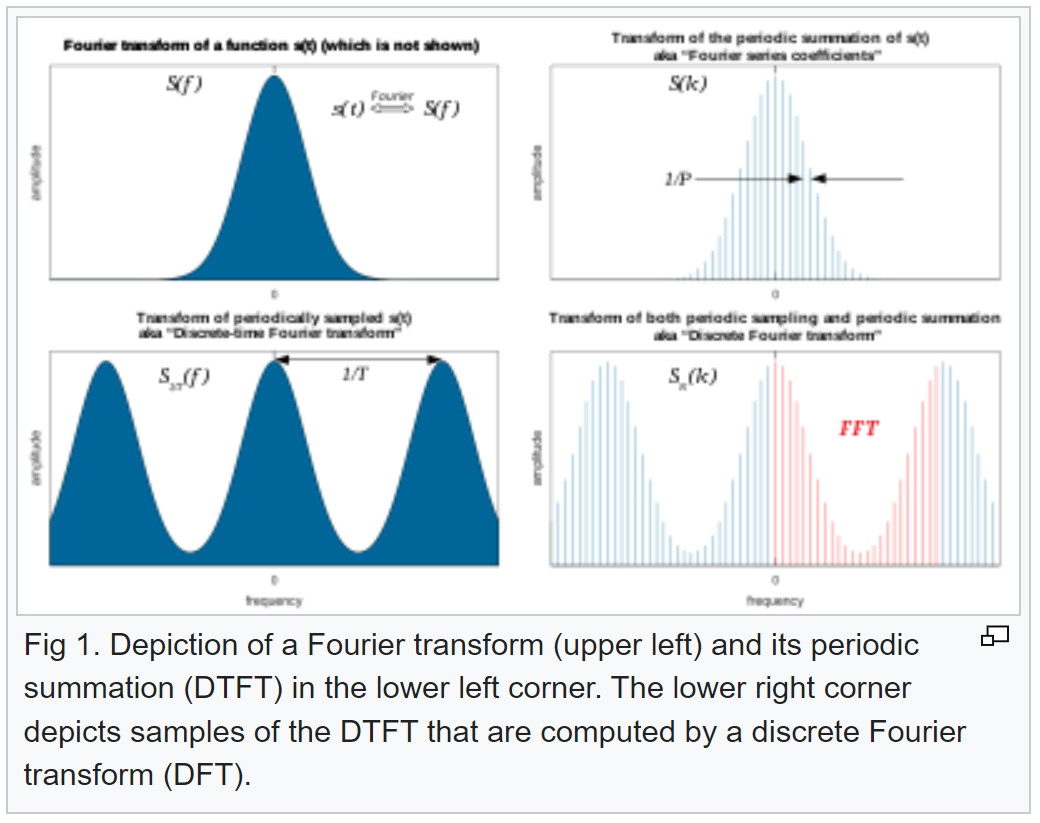
DTFT是無限長不可數信號的傅立葉表示方式 (由FT延伸而來，無限長，如上圖左下所示，左上為FT)，公式如下：

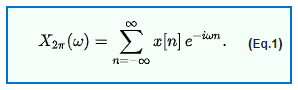
DFT是無限長可數信號的傅立葉表示方式 (由DTFT延伸而來，對DTFT取樣，如上圖右下所示，加速運算衍生FFT)，公式如下：

補充DTFT與DFT的表示：
STFT則是用short-time為單位來套用FT，這裡的FT可以是連續的FT也可以是DTFT，而一般實作上則是指DFT，而DFT往往又會被FFT取代。
FT演進史：

從Complex Form頻譜回推大小與相位 (The Meaning of Complex Form of DFT)

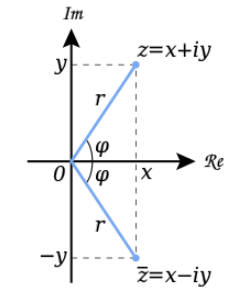
根據complex number的理論，要取得複數的大小會套用歐幾里得公式：將實部與虛部個別平方相加開根號。而取得複數的相位則是透過向量角度的取法：透過實部與虛部的長度反求對應的角度。

關於相位的解釋可以回想sin波所對應的相位變化，就能比較容易理解相位可以視為「波」的另一種形式表示法。這種表示方式是將一個數字能量拆開成實部與虛部，對應到複數空間就能看出相位的變化，透過實部與虛部的計算也能反推回原始波的能量大小或變化。

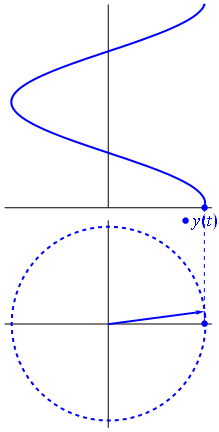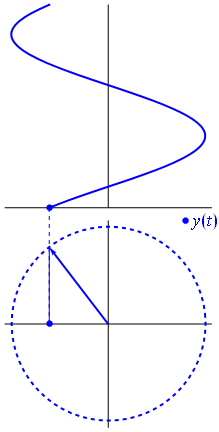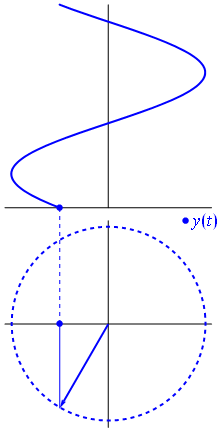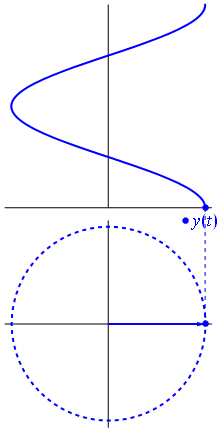
從Sliding Window的角度拆解STFT/ISTFT的運算過程

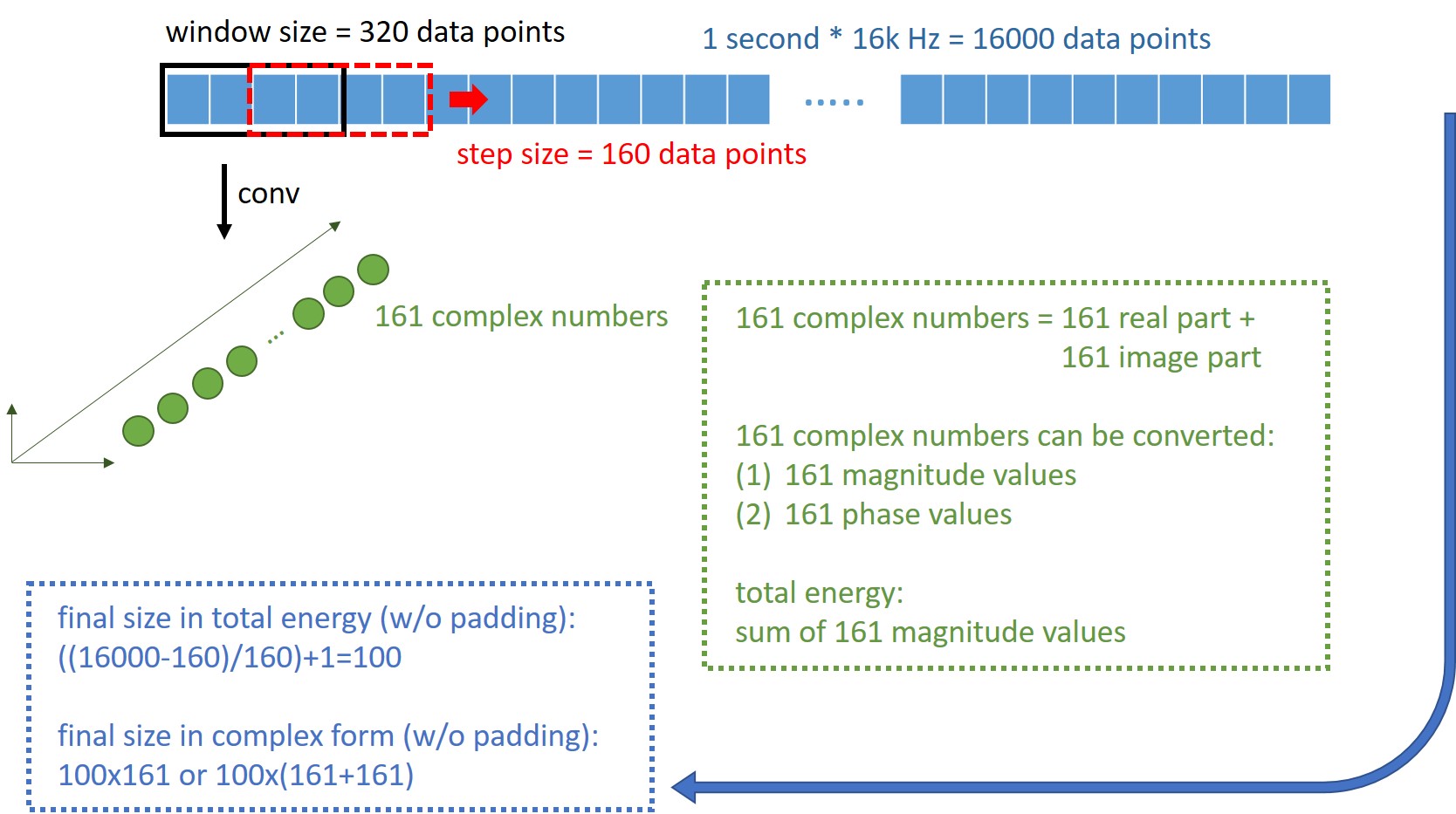
要注意的是，conv這個運算代表一組傅立葉轉換，用conv想表示其實這裡頭還隱含著另一個Sliding Window，裡頭的looping結束之後才會得到圖片中的綠色結果。

Convolution的概念可以參考以下：

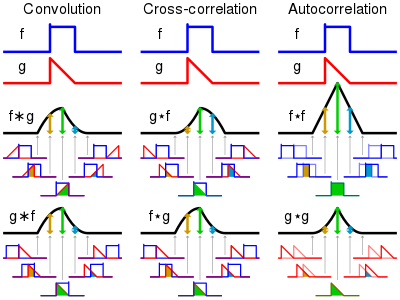
Inverse STFT (ISTFT)

概念上，STFT取Short-Time作FFT，但是仔細想想看，每組Short-Time作FFT的時候 (參考上圖Conv的運作)，其實兩邊都會補0，而非全都充滿著實際訊號。所以在作ISTFT的時候也是同樣道理，Short-Time區間所還原出來的訊號，越靠近邊界的訊號，成分越不完全，但是隨著Sliding Window的小步移動，恰好補足了邊界訊號所缺失的成分，透過疊加這一系列的結果，最終能夠還原出原始訊號。

或許從數學式子更能理解，但直接看圖片也是不錯的方式，下圖的解析就不錯 (圖片取自MATLAB)：

給自己的筆記：傅立葉轉換

Note of Discrete Fourier Transform (DFT)

目錄

DFT與DTFT的差異

從Complex Form頻譜回推大小與相位 (The Meaning of Complex Form of DFT)

從Sliding Window的角度拆解STFT/ISTFT的運算過程

Inverse STFT (ISTFT)

Reference